| DATA ANALYTICS REFERENCE DOCUMENT |
|
|---|---|
| Document Title: | Dynamic programming questions with solutions and detailed explanations |
| Document No.: | 1594121056 |
| Author(s): | Gerhard van der Linde |
| Contributor(s): | |
REVISION HISTORY
| Revision | Details of Modification(s) | Reason for modification | Date | By |
|---|---|---|---|---|
| 0 | Draft release | Document the collection of dynamic programming problems and solutions in python code | 2020/07/07 11:24 | Gerhard van der Linde |
Dynamic Programming Questions
Dynamic programming questions pops up in interview situations with the big technology companies and is used to asses analytical thinking and algorithm problem solving.
- Longest Common Subsequence
- Longest Increasing Subsequence
- Edit Distance
- Minimum Partition
- Ways to Cover a Distance
- Longest Path In Matrix
- Subset Sum Problem
- Optimal Strategy for a Game
- 0-1 Knapsack Problem
- Boolean Parenthesization Problem
- Shortest Common Supersequence
- Matrix Chain Multiplication
- Partition problem
- Rod Cutting
- Coin change problem
- Word Break Problem
- Maximal Product when Cutting Rope
- Dice Throw Problem
- Box Stacking
- Egg Dropping Puzzle
Longest Common Subsequence
# Longest Common Subsequence # LCS Problem Statement: Given two sequences, find the length of # longest subsequence present in both of them. A subsequence is a # sequence that appears in the same relative order, but not # necessarily contiguous. For example, “abc”, “abg”, “bdf”, # “aeg”, ‘”acefg”, .. etc are subsequences of “abcdefg”. s=('ABCDGH') t=('AEDFHR') step=2 def lcs(X, Y, m, n): # naive if m == 0 or n == 0: return 0; elif X[m-1] == Y[n-1]: return 1 + lcs(X, Y, m-1, n-1); else: return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n)); def lcs_d(X , Y): # find the length of the strings m = len(X) n = len(Y) # declaring the array for storing the dp values L = [[None]*(n+1) for i in range(m+1)] '''Following steps build L[m+1][n+1] in bottom up fashion Note: L[i][j] contains length of LCS of X[0..i-1] and Y[0..j-1]''' for i in range(m+1): for j in range(n+1): if i == 0 or j == 0 : L[i][j] = 0 elif X[i-1] == Y[j-1]: L[i][j] = L[i-1][j-1]+1 else: L[i][j] = max(L[i-1][j] , L[i][j-1]) # L[m][n] contains the length of LCS of X[0..n-1] & Y[0..m-1] return L[m][n] #end of function lcs print(lcs(s,t,len(s),len(t))) print(lcs_d(s,t))
Longest Increasing Subsequence
TestList: [22, 33, 55, 42, 63, 31, 44, 82, 84, 96] Result: 7 --> [22, 33, 55, 63, 82, 84, 96]
| Arr[] | 22 | 33 | 55 | 42 | 63 | 31 | 44 | 82 | 84 | 96 |
|---|---|---|---|---|---|---|---|---|---|---|
| LIS | 1 | 2 | 3 | - | 4 | - | - | 5 | 6 | 7 |
# Longest Increasing Subsequence import numpy as np def lis(): #n=[10, 22, 9, 33, 21, 50, 41, 60, 80] n=list(np.random.randint(1,100,10)) #print(n) test={} # create an empty library for the tests for i in range(len(n)): #print() seq=[] seq.append(n[i]) big=n[i] for j in range(i,len(n)): #print(i,j) if n[j]>big: seq.append(n[j]) big=n[j] #print(seq) test[i]=seq return test # find the longest list for i in range(1000): test=lis() l=test[list(map(lambda x: len(x),test.values())).index(max(list(map(lambda x: len(x),test.values()))))] if len(l) > 5: print(len(l),'-->',l)
Edit Distance
Given two strings str1 and str2 using the lister operations that can performed on str1. Find minimum number of edits (operations) required to convert ‘str1’ into ‘str2’.
- Insert
- Remove
- Replace
All of the above operations are of equal cost.
Examples: Input: str1 = "geek", str2 = "gesek" utput: 1 Comment: We can convert str1 into str2 by inserting a 's'.
The Levenshtein distance is a string metric for measuring the difference between two sequences. Informally, the Levenshtein distance between two words is the minimum number of single-character edits (insertions, deletions or substitutions) required to change one word into the other. It is named after the Soviet mathematician Vladimir Levenshtein, who considered this distance in 1965.
$$\Large lev_{a,b}(i,j)=\begin{cases} max(i,j) & \text if min(i,j)=0 & min \begin{cases} lev _{a,b}(i-1,j)+1 & & lev _{a,b}(i,j-1)+1 & & lev _{a,b}(i-1,j-1)+1 & \end{cases} & \text otherwise. \end{cases}$$
Levenshtein distance may also be referred to as edit distance, although that term may also denote a larger family of distance metrics known collectively as edit distance. It is closely related to pairwise string alignments.
| y | x | |||||
| g | e | e | k | |||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | ||
| g | 1 | 0 | 1 | 2 | 3 | |
| e | 2 | 1 | 0 | 1 | 2 | |
| s | 3 | 2 | 1 | 1 | 2 | |
| e | 4 | 3 | 2 | 1 | 2 | |
| k | 5 | 4 | 3 | 2 | 1 | |
So for every row and column there is only two cases:
- The pair match
- The pair do not match
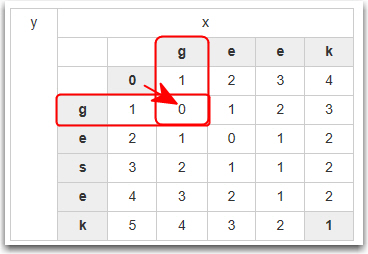
If the pair match copy the diagonal value across

If the pair do not match, take the smallest of the three values highlighted and add 1.
Implementation in Python using Matrixes
import numpy as np def getEditLen(inw, outw, verbose=False): ''' return the Levenstein distance between two word using the Levenstein formula implemented in python using a numpy array. input: Two strings to compare, example 'geek' and 'gesek' output: The number of edits required using insert, delete or replace to turn the input word into the output word. opetions: verbose=False|True, default is False Example: Calculate the distance between 'geek' and 'gesek' Compare the entire matrix row by row, starting with null cases answering the fundamental question for line g, how many edits is needed to turn g into g, g into ge, g into gee and g into geek and the answers would be 0,1,2,3 and so on. The second way to answer the question for every cell is, are the letters different or are the matched. If matched copy the value to the top left cell diagonally down. If the letters are different determine the lowest value of the three cell, left, top or diagonal left plus one to the cell. Keep on doing this till all the cells are filled. | | |g|e|e|k| | |0|1|2|3|4| |g|1|0|1|2|3| |e|2|1|0|1|2| |s|3|2|1|1|2| |e|4|3|2|1|2| |k|5|4|3|2|1| The final answer to the problem is now in the bottom right cell and can be returned by the function call. ''' # create an empty array for storing results #get the arary dimensions liw=len(inw) low=len(outw) #create an empty array ar=np.zeros((liw+1,low+1), dtype=np.int) #initialise the null array rows and columns for i in range(low+1): ar[0][i]=i for i in range(liw+1): ar[i][0]=i if verbose: print(ar) for i in range(len(inw)): row=i+1 for o in range(len(outw)): col=o+1 if verbose: print('{}[{}] == {}[{}] --> '.format(inw[i],i,outw[o],o), end='') if inw[i] == outw[o]: # if the letters match do this if verbose: print('True',' -->', ar[row-1][col-1]) ar[row][col]=ar[row-1][col-1] # copy the value diagonally down, i.e one row up, one columen left else: # if the letters do not match, do this part if verbose: print('False','-->',min(ar[row-1][col],ar[row][col-1],ar[row-1][col-1])+1) # set te smallest value of the three columns, left, above or between plus one. ar[row][col]=min(ar[row-1][col],ar[row][col-1],ar[row-1][col-1])+1 if verbose: print(ar) return ar[-1][-1] # return the bottom right value as the final answer. if __name__ == '__main__': wlen=getEditLen('geek', 'gesek', verbose=False) print('The Levenstein length is: {}'.format(wlen))
References
Minimum Partition
The objective of this exercise is to create two lists from once list of values and divide them in such a way that the difference of the sum of each list is the smallest possible solution for the numbers available.
With a short list of numbers a more thorough comparison is needed and all possible permutations must be tested to get the minimum difference. As the list size is increased a faster approach is needed for time efficiency and also the need to compare all permutation is no longer needed since multiple solutions becomes available.
A short solution for longer lists is to sort tow lists is ascending and descending order and subtract the one for the other and find the nearest solution to the sum of differences and swop the values around in the list to get the minimum error.
Testing this over a ranges of lengths works without fail.
The code below show the two tiered approach for this solution and includes time efficiencies generating the solutions.
import numpy as np from time import time def split(l): ''' This function sorts the list from small to big and devide into two lists of equal length. input: a list of variables output: two lists of variables of very similar sums ''' l.sort() a,b=[],[] for i in range(len(l)): if i%2==0: a.append(l[i]) else: b.append(l[i]) return a,b def bestdiff(a,b,verbose=False): ''' This function takes two lists of integer values and balances the list to be a close as possible to equal sums or in other words to have the minimum difference in sums. Inputs: Two lists in integeres and verbose processing or not, default off Outputs: Two balanced lists of integeres and a flag for the fast or slow method. The slow method is more accurate and needed for very short lists while the fast method is best suited for longer lists. Lists over 1000 values in length takes very long to comlete using the slow method and does not yiled better results. ''' tlen=len(a)+len(b) # total length of both lists if verbose: print('Lengt of testarray: {}'.format(tlen)) t=(sum(a)-sum(b)) # caalculate the delta between the lists entered if verbose: print(t/2) # show the half of the delta if t < 0: # if the delta is smaer than zero swop lists a and b b,a=a,b d=[int((i-j)-(t/2)) for i,j in zip(a,b)] # calculate the list differences b.sort() # sort the list a.sort(reverse=True) #sort in reveres if verbose: print(a) if verbose: print(b) m,p=[],[] if tlen <=2**9: # if the list is smaller than 2^9, 512 do a thorough comparison fast=False # find the values closes to the delta and swop to make list sums equal or nearest equal for i in range(len(a)): for j in range(len(b)): v=a[i]-b[j]-int(abs(t/2)) if verbose: print('{:>2} - {:>2} = {:>3} <-- {} {}'.format(a[i],b[j],v,i,j)) m.append(abs(v)) p.append((i,j)) i,j=p[m.index(min(m))] #swop the values around else: # otherwise if buger than 512 len do a faster compare fast=True t=(sum(a)-sum(b)) d=[int((i-j)-(t/2)) for i,j in zip(a,b)] e=[abs(i) for i in d] #print(min(e),e.index(min(e))) i,j=e.index(min(e)),e.index(min(e)) if verbose: print(m,min(m),m.index(min(m))) if verbose: print(p[m.index(min(m))]) #i,j=p[m.index(min(m))] a[i],b[j]=b[j],a[i] # swop the values around return a,b,fast if __name__ == '__main__': # generate a range of numbers for increased list lengths for testing r=[2**i for i in range(2,21)] # 4 to 1 Million for v in r: #print(v) start=time() # start the time l=list(np.random.randint(1,100,v)) # generate a list of values for testing a,b=split(l) # split the list of values in tow sublists a,b,s = bestdiff(a,b) # return the best solution stop=time() # stop the timer #display the results t=stop-start if t < 0.5: t*=1000 st='ms' else: t*=1 st='s' print('diff: {2:>3} len: {4:>9,} time: {3:8.3f} {5:>2} fast: {6:}'.format(a,b,sum(a)-sum(b),t,v,st,s))
diff: 26 len: 4 time: 0.496 ms fast: False diff: 3 len: 8 time: 0.000 ms fast: False diff: -1 len: 16 time: 0.495 ms fast: False diff: 1 len: 32 time: 0.992 ms fast: False diff: 1 len: 64 time: 3.965 ms fast: False diff: 0 len: 128 time: 13.399 ms fast: False diff: 0 len: 256 time: 32.237 ms fast: False diff: 0 len: 512 time: 4.465 ms fast: True diff: -1 len: 1,024 time: 8.929 ms fast: True diff: 0 len: 2,048 time: 14.884 ms fast: True diff: 0 len: 4,096 time: 25.296 ms fast: True diff: 0 len: 8,192 time: 57.052 ms fast: True diff: 0 len: 16,384 time: 92.770 ms fast: True diff: -1 len: 32,768 time: 208.359 ms fast: True diff: 0 len: 65,536 time: 374.552 ms fast: True diff: -1 len: 131,072 time: 0.964 s fast: True diff: -1 len: 262,144 time: 1.631 s fast: True diff: -1 len: 524,288 time: 3.240 s fast: True diff: -1 len: 1,048,576 time: 5.768 s fast: True
Ways to Cover a Distance
Code
''' Count number of ways to cover a distance Given a distance ‘dist, count total number of ways to cover the distance with 1, 2 and 3 steps. Examples : Input: n = 3 Output: 4 Below are the four ways 1 step + 1 step + 1 step 1 step + 2 step 2 step + 1 step 3 step Input: n = 4 Output: 7 ''' import itertools as itr def uniquePermutations(inv): return list(set(itr.permutations(inv,len(inv)))) def calcdist(n=3,steps=(1,2,3), verbose=False): p=[] if n>10: print('n need to be less than 10') return -1,p for i in range(1,n+1): l=list(itr.combinations_with_replacement(steps,i)) for v in l: if sum(v)==n: if verbose: print('{}: {}-->{}'.format(i,v,sum(v))) p.append(v) if len(v)>1: u=uniquePermutations(v) for q in u: if verbose: print(q) p.append(q) return len(list(set(p))), list(set(p)) if __name__ == '__main__': #for i in range(1,10): for i in range(11): ways,steplist=calcdist(i) if i<7: print('{}: {:>2} --> {}'.format(i,ways,steplist)) else: print('{}: {:>2} --> '.format(i,ways,steplist))
Output
0: 0 --> [] 1: 1 --> [(1,)] 2: 2 --> [(2,), (1, 1)] 3: 4 --> [(1, 2), (1, 1, 1), (3,), (2, 1)] 4: 7 --> [(1, 2, 1), (1, 3), (3, 1), (2, 1, 1), (1, 1, 1, 1), (1, 1, 2), (2, 2)] 5: 13 --> [(3, 2), (3, 1, 1), (1, 1, 3), (1, 2, 2), (2, 2, 1), (1, 1, 2, 1), (1, 3, 1), (2, 1, 1, 1), (1, 2, 1, 1), (2, 3), (2, 1, 2), (1, 1, 1, 2), (1, 1, 1, 1, 1)] 6: 24 --> [(2, 2, 1, 1), (1, 3, 2), (1, 1, 1, 2, 1), (1, 1, 2, 1, 1), (1, 1, 3, 1), (2, 3, 1), (1, 1, 2, 2), (2, 1, 2, 1), (3, 3), (1, 2, 2, 1), (3, 1, 1, 1), (3, 1, 2), (1, 2, 1, 1, 1), (1, 1, 1, 1, 1, 1), (1, 2, 1, 2), (3, 2, 1), (2, 1, 1, 2), (1, 2, 3), (1, 1, 1, 1, 2), (1, 3, 1, 1), (2, 1, 3), (1, 1, 1, 3), (2, 2, 2), (2, 1, 1, 1, 1)] 7: 44 --> 8: 81 --> 9: 149 --> 10: 274 -->
